Portal Engines

Portal engines are great for rendering inside environments, since they are based on the notion of only rendering areas that can be seen through openings (portals). The shape of the visible area changes as it passes through each portal and eventually fails to see any more portals, at which point the algorithm stops. With a little algebraic trickery, a portal can also double as a mirror.

Here's an example:

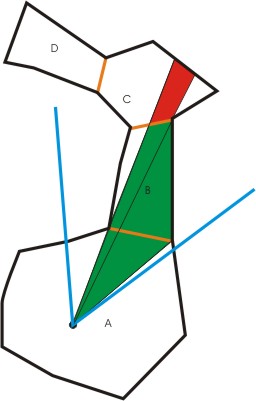
The viewpoint is in room A, with the viewport frustum defined as the two blue lines. The orange lines represent portals. The viewport frustum can see the portal leading to room B, so it reduces the frustum to the green area and looks for visible portals in Room B. It sees one at the far end and reduces the frustum to the red area and looks for visible portals in room C. It doesn't see any there, so it renders room C, then B, then A. And we're done.

What you need

In order to get a portal algorithm going, you'll need to start with some guidelines on how to define your environment:

Surfaces and portals should be defined in the same direction (clockwise or counterclockwise) so that their normals are similar as well. Surface segments should have a unit segment along their length, length of the segment itself, and a segment normal that points into the surface to speed up some calculations.

It is also possible to define two alpha blended surfaces to oppose each other - that is, they make up a two-sided alpha surface. This is important for applying decals that would be visible on each side, but that's another discussion. This isn't an article about applying decals, it's for a portal engine. Just something to keep in mind.

It isn't necessary to define every room as convex (no pointy parts) if you're using depth testing hardware, although the surfaces should be convex planes (for easy submission to the rendering routines), and the portals MUST be (for generation of valid frustums). So if you want a portal that is concave, compose it of adjacent convex polygons, each a different portal.

Also, if you plan to have any mirrors, make sure the algorithm tests mirrors in the same room that would occlude others first (define them first in the adjacent portal list for any given room).

It would be wise to have texture mapping be as uniform as possible on the mirrors, since it's likely they will be spliced by a frustum, and you'll need to be able to calculate new texture coordinates for a nice render.

The algorithm

In basic terms, the algorithm goes like this:

Start in the room where the viewpoint is, and a frustum defining the visible viewport.

This causes the room's contents to be rendered last in a back to front method. This would allow you to use a painter's algorithm of you want to avoid any depth testing at all, but that would only work if your rooms are defined as convex. If you have any wall angles greater than 180 degrees, you better use depth testing.

Incorporating mirrors, the algorithm turns into this:

Start in the room where the viewpoint is, and a frustum defining the visible viewport.

As you can see, there is a lot of preparation for rendering mirrored surfaces. A stencil is required so that the mirror's image doesn't cut into the viewport's depth buffer outside of the mirror's visible bounds. The clip plane keeps geometry from reaching out of the mirror itself. The depth masking of the mirror surface afterwards prevents anything else from cutting into the rendered mirror image. It is important for mirror surfaces to be parsed and rendered first, front to back, to avoid corruption of their images by future rendering (including mirrors encountered deeper in the parse). Also note that only one active clip plane is necessary, since you can store and restore clip planes as each mirror parse completes.

Now for a little discussion:

As a final note, since it's possible for a room to be parsed more than once during rendering (imagine a long hallway with multiple doorways, and you are in a long room looking at two of those doorways), you should ensure that each room is only rendered once and in the proper order. I keep a list of room ID's and keep track of the very last room I parsed from. When it's time to render the room according to the algorithm, I just add that room's ID directly after the last room's ID in the list (if it isn't already there). Then, when all parsing is done, I just render the rooms from the end of the list to the front. This way, it's a true back to front render with single room draws, even if I've parsed a room twice.

Portal visibility challenges

I listed some generalized cases that imply portal visibility in the algorithm discussion above, but there is one case that floating point truncation fails to address: If a portal's points and segments are such that they coincide exactly with a frustum's plane intersections, the calculations may fail to yield an accurate result. There are at least two possibilities of getting around this problem, but they can be computationally expensive (at least, the first one is, the second one might actually save you some processing):

Splicing a polygon with a frustum

This isn't the fastest way for certain, but it works.

Prepare an array of vertices and pass it to the splicer. Also provide a planar normal and a point on that plane. The routine returns a new array of points that make up the spliced polygon (It keeps all the points in front, and adds a single exit and entry point for the group of vertices that are in back, if any). Repeat for every plane in the frustum, and your end result is the spliced polygon. Watch for 0 vertices being returned, signifying a null result.

This routine could be written better to avoid passing back arrays of points repeatedly (in other words, make it a single pass routine), but you'd somehow have to ensure that your planes are adjacent to each other in the frustum, and that none are extraneous. That way you could follow the planes and polygon around and splice up the polygon in one pass. I'm holding off on writing that algorithm myself. I wrote a one-pass polygon-polygon intersection routine for applying decals to surfaces and got severely burnt out on that kind of logic.

As has been mentioned, you could pass a portal to this routine to determine if the portal is visible to that frustum. A null result means the portal isn't visible.

Some test cases

Here are some maps that might be useful to set up to make sure your portal engine is doing what it's supposed to. Note that if you have written a total polygon splice routine and use it for all rendering, you likely won't run into many of the problems discussed here.

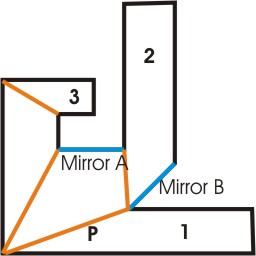
If you are at point P looking at Mirror A, you shouldn't see hallway 3 cutting into mirror A's rendered image (avoided by depth masking mirror A's surface after rendering it), and you shouldn't see mirror A's image of hallway 1 cutting into hallway 2 (avoided by stenciling mirror A's surface properly). Mirror B is there just for mirror-mirror testing.

 

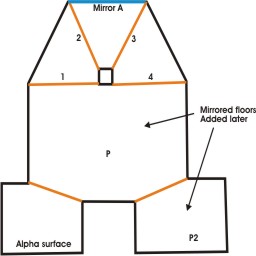
I originally made this map to test that mirror A's alpha surface wouldn't be rendered more than once when viewed from point P (its room is parsed twice by passing from the room with point P through portals 1 and 2, then 3 and 4, which causes the mirror's image and surface to be rendered twice by the algorithm - but proper stenciling of the mirror via the frustums avoided accumulation of the alpha surface). I also wanted to make sure the alpha surface at the lower left didn't accumulate (my algorithm only renders rooms once even though they may be parsed multiple times, which the alpha surface's room could be because of the post slicing the view down the middle).

After I added the two mirrored floors, however, I ran into some other problems. Suddenly, mirror A was sometimes being rendered multiple times, and it turned out that the frustums I was preparing as I passed through mirror portals were incomplete due to floating point truncations, causing slight failures that should have been successes. So, I allowed some tolerance in the frustum merging routine, and it took care of the problem. This tolerance might allow more planes in the frustum than I need, but at least that isn't a destructive result. It just results in extra superfluous planes to calculate against deeper into the algorithm.

Another problem I had after adding the mirrored floors was that portions of some mirrored surfaces would simply fail to render. I believe this was related to frustum planes that were almost coincident with the points and segments of a portal, which caused accuracy problems with the portal visibility algorithm. I tried adding some tolerance to that routine, but it didn't totally fix the problem, and created others (for some strange reason, some mirrors would render their images but failed to render the alpha surface on the mirror itself). It mostly happened from point P2 while near the floor looking into the main room. I altered the code to test for visibility by testing all the vertices, and if all those fail, just submit the portal for splicing. If I get a non-null result, the portal is visible. I set a control in my code to activate that test when I could see the first test failing, and the new code fixed it.

Other test ideas

In my code, I actually set an initial frustum to be very narrow and rendered an alpha quad that represented its bounds in the viewport to see the result when it intersects portals. It was a handy way to troubleshoot specific cases. When dealing with mirrors, it was be interesting to see how everything within a mirror was rendered but everything outside the quad on the mirror will be blank, and random other pieces of geometry outside the quad will be seen from rooms that were rendered unstenciled.

Avoiding artifacting

For the most part, if you're using hardware acceleration and aren't splicing every polygon with frustums for rendering, the only time you'll have to worry about artifacting is with mirrors. And so far, what I've seen is slight. If you want to see how bad it can get for you, set up a room with a square post in the center, and 4 rooms and portals around it. Then move around the room and see if you're satisfied with the results.

By using the same vertex values for adjacent surface segments, you avoid most artifacting problems. However, mirrors present a new problem. If the flip on the mirror plane isn't exact (nothing is exact in computers), there may be some artifacting on the edges of the mirror surface. It will be very noticable if you clear the screen to a noticable color before you beging your rendering. I like 128,128,128 gray myself. The dots still appear here and there, but they aren't horribly obvious. That might change in a very dark room, though. I recently changed the value to 0,0,0 black to avoid gray dots appearing in the darkness.

Another problem I ran into originally was Z fighting on the alpha surfaces of mirrors, because I was rendering those surfaces with the room walls after depth masking the mirror surface. After I coded to have the mirror parse routine render its depth mask and alpha surface at the same time, I avoided having to solve that problem (originally I tried receding the depth mask a little inside the mirror, but then it was visible around hard corners. The way I finally solved it is more complete).

One tweak I do perform to reduce artifacting with mirrors is recede the viewpoint slightly when I flip it. The rendered image inside might foward by a minute amount, but it's something.

One theory about artifacting I have yet to fully explore is the idea of same input, same output. I figure if I can guarantee that all segments and vectors are heading in the same direction (x always positive, if x = 0 then y is always positive, if y = 0 then z is always positive, reverse the vector to accomplish this), maybe I can make sure they always generate similar results. To further enforce it, I would hold on to spliced segments for use at the end of a routine, but the source segment would be retained and used in all calculations where that segment is involved. That way, there aren't any second, third, or greater generation truncations on the same segment occurring. But, that's a bit off, and I don't even know if it will work. Still, a room with many adjacent mirrored surfaces sharing many segments might be a good test.

The main places where this kind of control would be needed is in polygon splicing, frustum merging, and in whatever way it can apply, flipping the rendering transformation.

Polygon splicing is always done with a frustum and an original surface. The frustum planes only come from the original viewport frustum and plane made from original portal segments. So it seems the only place where second generation truncation could occur is in the polygon splice routine. The same segment could be spliced multiple times by different planes. Using the original segment for calculation of all splices would keep the truncation at a minimum instead of letting it get worse.

Frustum merging is just a matter of keeping or getting rid of planes that came from original sources, so assuming the originals are accurate, this shouldn't be an issue. The directions of vectors used to generate planar normals could be controlled.

Ensuring that flipping the rendering transformation is accurate could be as simple as using double floats instead of singles. Multiple flips could occur, so perhaps it would be prudent to hold on to those values and pass them on.

Also make sure you push and pop values or copy them from storage rather than "calculate them back". As an example, I ran into a situation where I spliced a mirror and prepared a stencil, but tried to restore the stencil by rendering the original surface rather than the splice. I got intermittent pixels that didn't unstencil. Restoring the stencil by using the splice fixed the problem.

Funky mirrors

If you don't do mirrors right, you can really get some strange results.

I previously thought that it was ok to have multiple mirrors in the same room as long as the mirrors are defined in order of occlusion. But there is one possibility I recently considered. If you have two mirrors opposite each other and stand in front of one, your position will flip in front of the other mirror for rendering. And since the rendering of a mirror's image starts in the same room of the mirror itself, the new viewpoint will see the mirror on the other side and work with that. I can't testify that strange effects occur when this happens, since in my demo, I haven't seen anything strange happen as a result. But I can testify that the opposite mirror's portal was calculated as visible and caused another unnecessary (and realistically impossible) render. So, for safe keeping, if your mirrors are facing away from each other (facing opposite directions), you should probably split the room with a portal and define them as being in different rooms. Mirrors facing each other is fine, as long as they aren't more than 90 degrees off.

Another test

Just to make sure your portal evaluations, recursive logic and frustum mergings work correctly, here's another test map:

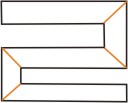
All angles are 90 degrees on the walls, and the portals are exactly 45 degrees. In order for this map to provide a test, you'll need collision detection. Slide into a corner so that you are lying exactly on a portal and make sure everything renders correctly (and you don't get an infinite loop).

Do rooms need to be convex?

It helps for determining if a point is inside a room by testing its position against the surface normals. A concave room could calculate a point being outside the room (see below). If you are rendering particles per room, then this becomes important - particles rendered per room are rendered more accurately with alpha walls, since they are supposed to be rendered first, then have the alpha wall blended over them. It's also important when you need to calculate which room the viewpoint is in to begin rendering, and you aren't determining the room you're in via a BSP or other structure.

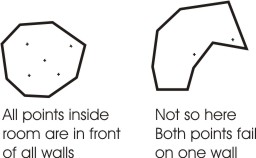
If you have ways of calculating if a point is inside a room without using the surface normals, then convex rooms may not be so necessary. It's up to the methods you make available for yourself.

Note that the portal rendering algorithm itself does not require convex rooms. Portal visibility requires that you are on the correct side of the portal to see it, and if the portal is around a corner in the same room, visibility fails. It's just the initial calculation of which room the viewpoint is in that might require it. If, however, your movement algorithm tracks passing through portals, you may be able to determine which room the viewpoint is in without testing against surface normals, assuming you can't pass through walls.

If you find that the way you do things does require convex rooms, fortunately you can always build convex rooms even if they are initially concave. Just splice the room with portals until all the room sections and portals are convex, and set it up that way.

Note that even though the rooms may not need to be convex, the portals do for accurate visibility and valid frustum merging. Mirrors especially should be convex, since the algorithm has to splice up a polygon to stencil.

If you are finding that your map designs are preventing you from making convex areas without overcomplicating the room and portal definitions, you can define other volumes meant to contain rooms and represent portals that stretch outside the visible geometry that will be rendered, and just use the other volumes to determine room containment and portal visibility. The visible geometry should properly occlude the outer edges of the larger portal, as long as the defined visible geometry for a room doesn't cross the portal's surface.

To illustrate, say you have a cavern and a jagged exit at one end. Stalagmites might be part of the visible geometry of the room, and the exit could be star-shaped. Setting up everything to be convex would probably require a lot of overdefinition. So define a large square portal to define the exit that extends into the surrounding walls, and define a large oval shape to contain the cavern (it could even be a cube, as long as no other rooms intersect).

What about everything else in the level? (Particles, light sources, doors, other objects)

The portal engine itself mostly is really only good for rendering the walls themselves. Where room containment can be calculated, particle rendering can be incorporated into it. But particles can be so numerous that calculating that they remain in the room as they move can be costly, so be careful.

However, light sources and objects can't be rendered purely by room containment, since there is size to them. They could easily exist in a room that isn't visible, but the object should still be visible (like a warrior holding a long lance poking through a door), and a light source should still be affecting other visible walls (a 40 foot radius light above the warrior should be lighting the wall inside the door).

I solve these kinds of problems using an octree. I keep track of which objects, lightsources, etc. that are touching each cell, and when I render a room, I refer to all the cells the room touches and render all the objects and use all the lightsources also touching those cells. Most of it is overapproximation (a warrior with a lance is treated like a huge cube, since it could have any orientation), but I'd rather get too much than too little.

The octree also assists with limiting collision detection parsing and faster calculation of which room a point is in (I figure out which cell a point is in and test the point against all the rooms touching that cell).

I maintain lists at both the cell level and object/light source/door/room levels and keep them updated in parallel as objects and light sources move. It works, for now.

So, to summarize, I've set up my portal engine as follows: